This was the first problem in last year's Junior Mathematical Olympiad, held in Veria, Greece. It was considerably easy, as it takes only a few simple observations. Let us start, shall we?
We can easily see that the inequality is cyclic, which means that it is the addition of the three following inequalities:
Since all three of them are identical, we can simply prove one and be done, since we would have to use the same method for the other two as well. So let's work on the first one.
From the hypothesis, we can say that
So the initial inequality can be written as:
Now this is the only part where the solution becomes a bit complex, so pay attention.
Using the AM-GM inequality, we have that:
Which means that we have proven the initial inequality. Using the same method, we can prove the other two inequalities. By adding the three inequalities together, we reach the given inequality. Obviously, equality holds if, and only if:


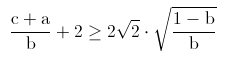





Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου