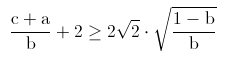Junior Balkan Mathematical Olympiad 2007 - Problem 3

This was the third problem of the JBMO 2007 held in Bulgaria. I find it very beautiful and I think it has a very elegant solution. Again, like all JBMO problems in my opinion, it only takes a few observations to reach a solution.

Using the Pigeon Hole Principle, we can express 50 in terms of 4. Like this:

From this statement, we can reach the conclusion that there are at least 13 points of the same colour in the plane.

Now, the key to solving this problem is to find out how many triangles we can create out of 13 points of the same colour and then reach more conclusions.

The amount of triangles we can create is equal to:

 Note that we would not be able to use this formula if it was not stated in the hypothesis that no three points are collinear.

What is left to prove, is that there exist at most 156 isosceles triangles, so that the remainder which is equal 130 will be scalene triangles.

Pay attention now, because this part is tricky.

Consider a segment created by two points. Then we can say that we can create at most 2 isosceles triangles per segment. The reason for that is that there can be at most 2 points belonging to the semi-perpendicular of that segment*. The semi-perpendicular of a segment is a straight line that bisects the segment and is perpendicular to it. Geometry tells us that the distances between any point on the semi-perpendicular of a segment and the points creating that segment are equal. For a better understanding, I have prepared a shape:

*That is due to the fact that no three points are collinear.

So now that we have proven that there can be up to 2 isosceles triangles created by a segment, we have to find the amount of segments we can create and multiply it by 2.

So the total amount of segments is 78. Should we multiply that by 2, we receive 156 isosceles triangles, which gives us 130 scalene triangles, as we wanted.

Junior Balkan Mathematical Olympiad 2012 - Problem 1

This was the first problem in last year's Junior Mathematical Olympiad, held in Veria, Greece. It was considerably easy, as it takes only a few simple observations. Let us start, shall we?

We can easily see that the inequality is cyclic, which means that it is the addition of the three following inequalities:

Since all three of them are identical, we can simply prove one and be done, since we would have to use the same method for the other two as well. So let's work on the first one.

From the hypothesis, we can say that

So the initial inequality can be written as:

Now this is the only part where the solution becomes a bit complex, so pay attention. 

Using the AM-GM inequality, we have that:

Which means that we have proven the initial inequality. Using the same method, we can prove the other two inequalities. By adding the three inequalities together, we reach the given inequality. Obviously, equality holds if, and only if:

Introductory Message

   Hello everybody! I am hoping to keep this message short enough so that it doesn't get boring. My name is Kleovoulos, I am 15 years old and I am from Greece. In this blog I will be trying to give solutions to mathematical problems from international competitions such as the Junior Balkan Mathematical Olympiad, the Balkan Mathematical Olympiad and the International Mathematical Olympiad. To whoever likes Mathematics, I am hoping that this blog will be useful, as I will be trying to provide solutions accessible by everyone. To those who don't like Mathematics, I am hoping that this blog will help you see what makes me like it and hopefully even inspire you. So, that's what I have to say for now, I hope you enjoy this blog.

 - Kleovoulos

EDIT: 2nd of August 2013

From now on, Demetres will be joining me as a moderator of this blog. He will also be posting problems from International Competitions. He has been successful in numerous competitions nation-wide and his favourite branch of mathematics is Number Theory. He hopes that you will enjoy the solutions he posts and find them useful.